链表中环的入口节点

题目描述

给一个链表，若其中包含环，请找出该链表的环的入口结点，否则，输出null。

分析

​ 假定存在一个链表并包含环，如果存在两个指针 p1、p2 同时出发但 p1 速度是 p2 的两倍。那么当两指针都进入环后，两指针终将相遇。如下图所示

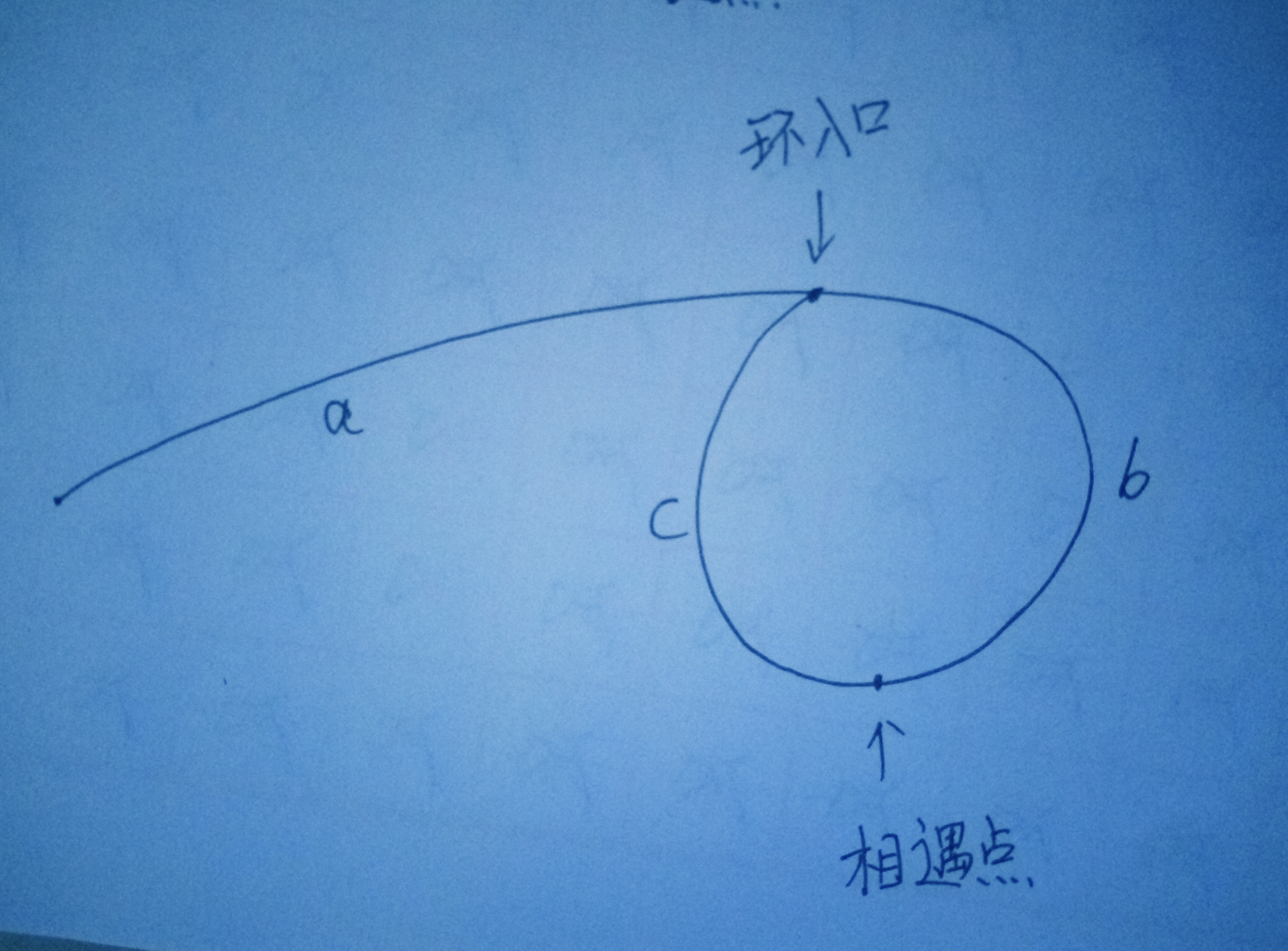
当相遇时有：

快指针 p1 路程 = a + (b + c)k + b , k >=1 其中 b + c 为环的周长，k为绕环的圈数。（最少一圈，不然和慢指针走的一样长，矛盾）

慢指针p2路程 = a+b

因快指针速度是慢指针的两倍，所以：

• （a+b)* 2 = a + (b + c)k + b
  • 化简可得： a = (k - 1)(b + c) + c

这个式子的意思是： 链表头到环入口的距离 = 相遇点到环入口的距离 + (k-1)倍的环周长。这说明两个指针如果分别从链表头和相遇点出发，最后一定相遇于环入口。

实现

public ListNode EntryNodeOfLoop(ListNode pHead)
    {
        ListNode fast = pHead;
        ListNode low = pHead;
        while(fast != null && fast.next != null){
            fast = fast.next.next;
            low = low.next;
            // 相遇
            if(fast == low)
                break;
        }
        if(fast == null||fast.next == null)
            return null;
            // 慢指针从链表头出发
        low = pHead;
        while(fast != low){
            fast = fast.next;
            low = low.next;
        }
        return low;
 }